Neve e aritmetica: come l’intensità della precipitazione influenza il limite della neve

La previsione delle nevicate costituisce una vera e propria “croce e delizia” per il meteorologo professionista, così come per i tanti appassionati della neve e degli sport invernali. Anche se esistono definizioni leggermente diverse fra loro il limite delle nevicate indica generalmente la quota oltre la quale la maggior parte della precipitazione cade sotto forma di neve. A questa altezza in generale non osserveremo un accumulo di neve al suolo poiché una parte della precipitazione è ancora  pioggia o neve molto bagnata; per osservare uno strato di neve dovremo spostarci verso l’alto di un centinaio di metri circa.

Il limite inferiore fino alla quale si spinge una nevicata dipende dal tipo di massa d’aria entro cui avviene la precipitazione. Nei casi più comuni in Italia lo zero termico (la quota oltre la quale le temperature sono pari a 0°C o negative) si trova ad alcune centinaia o migliaia di metri al di sopra del suolo.

Quando un fiocco di neve scende al di sotto del livello dello zero termico non fonde immediatamente, ma percorre ancora un po’ di strada prima di trasformarsi in pioggia: stimare la lunghezza di questo tragitto è sovente l’aspetto più sfidante della nostra previsione.

I fattori che condizionano questa lunghezza sono principalmente due: l’umidità dell’aria e l’intensità della nevicata. All’inizio di una nevicata la colonna d’aria sottostante allo  zero termico potrebbe non essere satura. In questo caso i cristalli di neve, anziché fondere, iniziano a sublimare (la sublimazione è l’equivalente per il ghiaccio dell’evaporazione per l’acqua) e il processo, che richiede energia, raffredda l’aria circostante fin tanto che essa raggiunge la saturazione (cioè un umidità relativa del 100%), ovvero fino a che la temperatura equivale alla cosiddetta temperatura di bulbo umido. Ecco quindi una prima regola per stimare il limite locale di una nevicata: se la nevicata prende avvio in aria secca osserveremo un graduale abbassamento dello zero termico (e del limite della nevicata) fino a che tutta la colonna d’aria non si sarà umidificata.

Questo effetto sarà tanto maggiore tanto più l’aria è inizialmente secca, ma il fenomeno, per quanto esposto, tenderà a esaurirsi ineluttabilmente (a meno che non si abbia a che fare con precipitazioni estremamente deboli) una volta raggiunta la saturazione dell’aria.

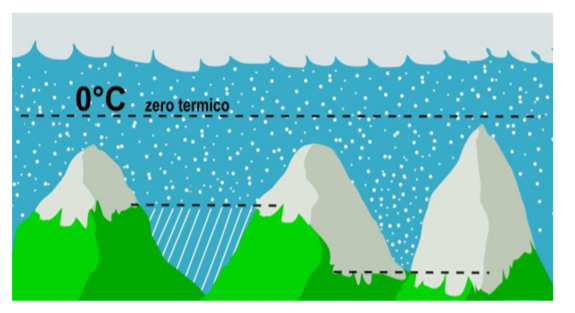
L’intensità e la durata di una precipitazione sono invece i fattori che, tramite l’effetto della fusione, influenzano in modo assai più deciso il limite di una nevicata, come mostriamo a breve con dei semplici calcoli. Capiremo come sia possibile che la neve riesca a cadere abbondantemente anche fino a 1000 m al di sotto del livello dello zero termico, particolarmente nelle vallate più strette, a causa del calore sottratto all’aria dal processo di fusione della neve che la attraversa.

Per questo semplice esercizio immaginiamo una precipitazione di intensità, per definizione moderata, di 4 mm all’ora o, se preferite, di 4 litri per metro quadrato ogni ora. Il termine “moderato” non tragga in inganno, in quanto 4 mm all’ora corrispondono ad un accumulo molto significativo di quasi 100 mm in un giorno. Immaginiamo come semplice ipotesi di lavoro che l’atmosfera sia satura, di trovarci nella parte bassa della troposfera e che il fiocco di neve impieghi 500 m per fondere (un valore arbitrario, ma realistico). La colonna d’aria avente per base un metro quadrato in un’ora verrà quindi attraversata da 4 litri d’acqua (o Kg, che è lo stesso poiché un litro d’acqua pesa un Kg)  che passeranno dallo stato solido a quello liquido assorbendo energia dall’aria stessa. Con una semplice moltiplicazione e conoscendo il valore del calore latente di fusione del ghiaccio troviamo che per fondere 4 kilogrammi di ghiaccio sono necessari 1340 KJ (Kilo Joule) di energia. Questa è l’energia che verrà assorbita dalla nostra colonna d’aria alta 500 m avente per base un metro quadrato.  Questa colonna, ipotizzando di essere nella parte bassa della troposfera, pesa circa 650 Kg (cioè il peso di un metro cubo d’aria, circa 1.3 Kg, moltiplicato per 500). Siamo quasi alla fine. Ad ogni Kg d’aria, in media, il processo di fusione sottrarrà quindi circa 2 kJ di energia (cifra ottenuta dividendo l’energia totale, 1340 KJ, per la massa della colonna d’aria, 650 Kg). A questo punto non resta che calcolare di quanto si abbassa la temperatura assoluta T di questo Kg d’aria ai quali sono stati sottratti circa 2 KJ di energia. Per farlo è sufficiente conoscere il valore del calore specifico dell’aria a pressione costante Cp (esso dipende leggermente dalla T stessa e dal contenuto di umidità, ma per i nostri scopi ciò è del tutto ininfluente) e la relazione che lega la variazione di temperatura dT all’energia assorbita Q:

 dT=Q/Cp

Cp vale circa 1 J/(Kg K) e per questo conto, poiché Q è circa 2KJ, non serve proprio la calcolatrice tascabile: la variazione di temperatura dT equivale a circa 2K!

Grazie a semplici leggi fisiche e all’uso di aritmetica elementare abbiamo mostrato che una precipitazione nevosa moderata che fonde in 500 m di caduta  abbassa la temperatura dell’aria di ben 2 gradi in una sola ora!

Questo risultato illustra la potenza del raffreddamento da fusione e spiega il fenomeno, regolarmente osservato, del graduale abbassamento del limite delle nevicate quando siano in atto precipitazioni intense e prolungate. Si tratta, si badi, di un risultato ottenuto immaginando una colonna d’aria ideale isolata rispetto all’ambiente circostante e per questo motivo l’effetto è particolarmente efficace nelle vallate alpine più strette circondate da alti rilievi: per cominciare nel fondo di queste valli il volume d’aria da raffreddare è minore; inoltre le alte cime circostanti la vallata impediscono all’aria più mite che scorre in quota di penetrarvi rimescolandosi con quella raffreddata dalla nevicata.